Basic points resulting from mixed radius
Keywords:
Abstract
Throughout this research, we present generating the correct points on the Pythagorean circle discussing the different cases of the radius that is defined by the following equation:
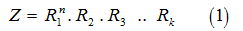
Where: 
are different prime Pythagorean numbers.
This research is going to create the fundamental points which generate the correct points in the circle. Besides, I am going to calculate the number of the correct points on the circumference of a circle in every different form of the equation (1) via the following:
- Depending on the laws and theorems resulted from this research.
- Depending on the computer program (C #) to yield fast and effective results.
We conclude by saying: We should take into account that the aim of this study is to pinpoint the nature and the number of the correct points on the circumference of a Pythagorean circle. As a result, we can exploit these points to decipher the data when they are transferred between users via unsecured nets. The current applied mechanism is to use elliptic curves which are complex and difficult to use if compared to the use of central Pythagorean circles due to its features and characteristics.
