النقاط الأساسية الناتجة من أنصاف أقطار مختلطة
الكلمات المفتاحية:
الملخص
خلال هذا البحث ، نقدم توليد النقاط الصحيحة على دائرة فيثاغورس لمناقشة الحالات المختلفة من نصف القطر المحدد بالمعادلة التالية:
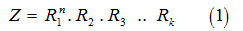
حيث: 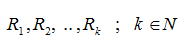 هي أعداد أولية مختلفة فيثاغورس.
هي أعداد أولية مختلفة فيثاغورس.
سيخلق هذا البحث النقاط الأساسية التي تولد النقاط الصحيحة في الدائرة. إلى جانب ذلك ، سأقوم بحساب عدد النقاط الصحيحة على محيط الدائرة في كل شكل مختلف من المعادلة (1) عبر ما يلي:
- بالاعتماد على القوانين والنظريات الناتجة عن هذا البحث.
- الاعتماد على برنامج الكمبيوتر (C #) لتحقيق نتائج سريعة وفعالة.
نختتم بالقول: يجب أن نأخذ في الاعتبار أن الهدف من هذه الدراسة هو تحديد طبيعة وعدد النقاط الصحيحة على محيط دائرة فيثاغورس. نتيجة لذلك ، يمكننا استغلال هذه النقاط لفك تشفير البيانات عندما يتم نقلها بين المستخدمين عبر شبكات غير آمنة. تتمثل الآلية المطبقة حاليًا في استخدام المنحنيات الإهليلجية المعقدة والتي يصعب استخدامها إذا ما قورنت باستخدام دوائر فيثاغورس المركزية نظرًا لخصائصها وخصائصها.













